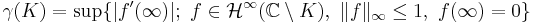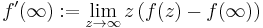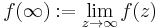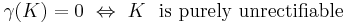Analytic capacity

In complex analysis, the analytic capacity of a compact subset K of the complex plane is a number that denotes "how big" a bounded analytic function from 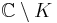\mathbb{C}\setminus K can become. Roughly speaking, 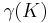\gamma(K) measures the size of the unit ball of the space of bounded analytic functions outside K.

It was first introduced by Ahlfors in the 1940s while studying the removability of singularities of bounded analytic functions.

Contents

Definition

Let 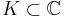K\subset\mathbb{C} be compact. Then its analytic capacity is defined to be

\gamma(K) = \sup \{|f'(\infty)|;\ f\in\mathcal{H}^\infty(\mathbb{C}\setminus K),\ \|f\|_\infty\leq 1,\ f(\infty)=0\}

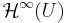Here, \mathcal{H}^\infty (U) denotes the set of bounded analytic functions 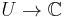U\to\mathbb{C} , whenever U is an open subset of the complex plane. Further,

f'(\infty):= \lim_{z\to\infty}z\left(f(z)-f(\infty)\right)
f(\infty):= \lim_{z\to\infty}f(z)

(note that usually 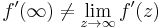f'(\infty)\neq \lim_{z\to\infty} f'(z) )

Ahlfors function

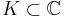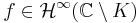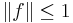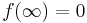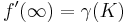For each compact K\subset\mathbb{C}, there exists a unique extremal function, i.e. f\in\mathcal{H}^\infty(\mathbb C\setminus K) such that \|f\|\leq 1, f(\infty)=0\, and f'(\infty)=\gamma(K)\,. This function is called the Ahlfors function of K. Its existence can be proved by using a normal family argument involving Montel's theorem.

Analytic capacity in terms of Hausdorff dimension

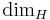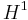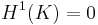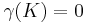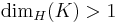Let \text{dim}_H denote Hausdorff dimension and H^1 denote 1-dimensional Hausdorff measure. Then H^1(K)=0 implies \gamma(K)=0 while \text{dim}_H(K)>1 guarantees 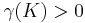\gamma(K)>0. However, the case when 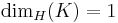\text{dim}_H(K)=1 and H^1(K)\in(0,\infty] is more difficult.

Positive length but zero analytic capacity

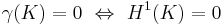Given the partial correspondence between the 1-dimensional Hausdorff measure of a compact subset of \mathbb{C} and its analytic capacity, it might be conjectured that \gamma(K)=0\ \Leftrightarrow\ H^1(K)=0. However, this conjecture is false. A counterexample was first given by A. G. Vitushkin, and a much simpler one by J. Garnett in his 1970 paper. This latter example is the linear four corners Cantor set, constructed as follows:

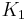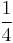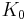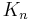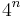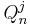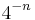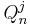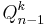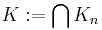
Let K_0:= [0,1]\times[0,1] be the unit square. Then, K_1 is the union of 4 squares of side length \frac{1}{4} and these squares are located in the corners of K_0. In general, K_n is the union of 4^n squares (denoted by Q_n^j) of side length 4^{-n}, each Q_n^j being in the corner of some Q_{n-1}^k. Put K:=\bigcap K_n

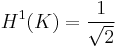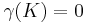
Then H^1(K)=\frac{1}{\sqrt{2}} but \gamma(K)=0

Vitushkin's Conjecture

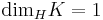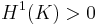Suppose \text{dim}_H K=1 and H^1(K)>0. Vitushkin's conjecture states that

\gamma(K)=0\ \Leftrightarrow\ K \ \text{ is purely unrectifiable}

In this setting, K is (purely) unrectifiable if and only if 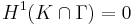H^1(K\cap\Gamma)=0 for all rectifiable curves (or equivalently, 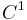C^1 -curves or (rotated) Lipschitz graphs) \Gamma.

Guy David published a proof in 1998 for the case when, in addition to the hypothesis above, 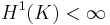H^1(K)<\infty. Until now, very little is known about the case when 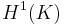H^1(K) is infinite (even sigma-finite).

Removable sets and Painlevé's problem

The compact set K is called removable if, whenever Ω is an open set containing K, every function which is bounded and holomorphic on the set Ω\K has an analytic extension to all of Ω. By Riemann's theorem for removable singularities, every singleton is removable. This motivated Painlevé to pose a more general question in 1880: "Which subsets of \mathbb{C} are removable?"

It is easy to see that K is removable if and only if 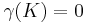\gamma(K)=0 . However, analytic capacity is a purely complex-analytic concept, and much more work needs to be done in order to obtain a more geometric characterization.

References